Etendue
Etendue is an essential concept mentioned many times in group meetings and biomedical optics classes. I did not pay attention to it until an informative discussion with our team. Credits to Indra, Josh, and Junhao.
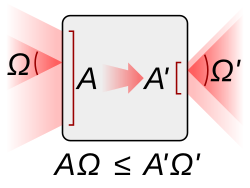
The root of etendue can be traced to statistical mechanics and Liouville’s theorem, which refers to incompressible volume in phase space. Here we present some intuitive understandings from optical systems.
Perspective of opcial imaging system
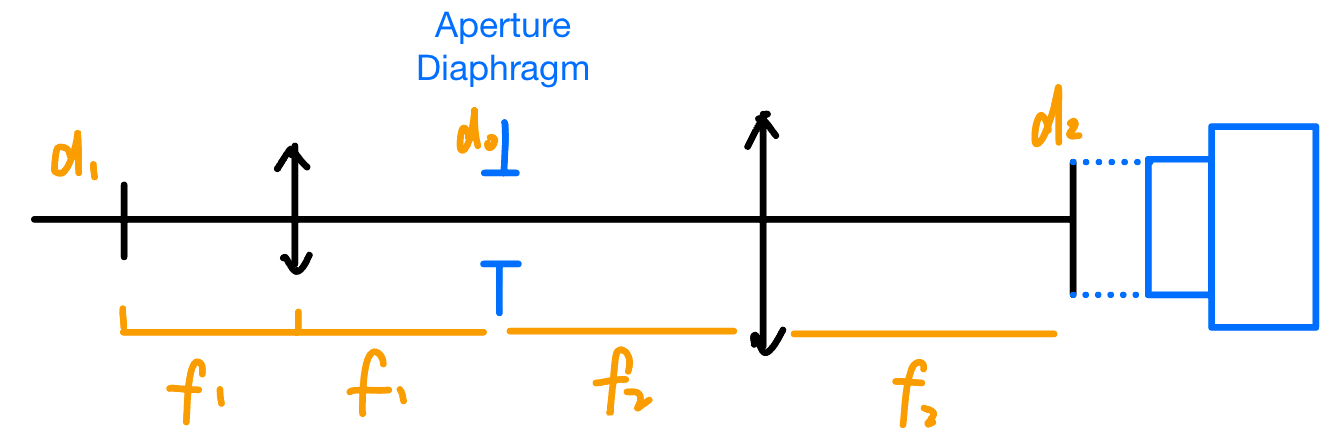
Given a 4f system, the magnification is: \[ |\mathrm{M}|=\frac{f_2}{f_1}=\frac{d_2}{d_1}, \] Therefore: \[ \frac{d_1}{f_1}=\frac{d_2}{f_2}. \] The aperture diaphragm gives the NA of the system: \[ \mathrm{NA} = \frac{d_0/2}{f_1}. \] Therefore, we have: \[ \boxed{d_1\cdot \mathrm{NA}_1=d_2\cdot \mathrm{NA}_2} \] This equation basically says that there is a trade-off between field of view (FOV) and resolution. Take the square on each side: \[ d_1^2\mathrm{NA}_1^2=d_2^2\mathrm{NA}_2^2\implies A_1\Omega_1=A_2\Omega_2, \] since the solid angle \(\Omega\) is defined by \(A/r^2\), which is equal to \(d_0^2/f^2\) in the system.
Perspective of information
The etendue \(A\cdot \Omega\) is the optical throughput received from the camera side. For small angles (paraxial approximation), we have: \(\mathrm{NA}\propto \sqrt{\Omega}\). Therefore, the camera sees: \[ N_{\mathrm{px}}=\frac{A}{\Delta p^2}\propto\frac{A}{(\lambda/\mathrm{NA})^2}=\frac{A\Omega}{\lambda^2}\propto \boxed{A\Omega}. \] The etendue is proportional to the total image pixels obtained by the camera, which is the terminal for the image system.